Chap2. 전지화학의 기본
- 전기화학 : 금속 또는 반도체 등의 전자반도체와 전해질 같은 이온전도체와의 계면에서 일어나는 산화 환원반응에 의한 전자전달을 다루는 학문
2-1 전지의 구성
전기화학 셀 및 전지
- 셀 : 화학 에너지를 전기 에너지로 변환하거나 그 반대로 전기 에너지를 화학 에너지로 변환하는 소재의 가장 작은 단위구조
- 2개의 서로 다른 전극과 전해질로 구성. 두 전극은 서로 다른 전위(electric potential)를 가져 전해질을 매개로 하여 연결되었을 때 전위차(기전력)가 발생한다.
- 전위 : 전기장 내에서 단위 전하가 받는 위치에너지
- 기전력에 의해서 각 전극에서는 산화, 환원반응이 일어나고 발생된 전자는 외부 회로를 통하여 이동한다.
- 이때 전해질에서는 전하중성을 유지하기 위하여 이온들이 두 전극 사이를 이동하여 셀이 전기화학적 평형에 도달할 때 까지 전극에서 산화 환원반응이 지속된다.
전지의 구성과 전극의 정의
- 전극(electrode)에서 전기화학적 산화환원반응이 일어날 때 전해질을 통하여 이온이 산화전극과 환원전극 사이를 이동하며, 동시에 도선을 통해 두 전극 사이에서 전자의 이동이 일어난다. → 폐회로
- 음극에서는 전지의 방전(discharge)동안 전극물질의 전기화학적 산화반응(oxidation, A → \(A^+ + e^- \))이 일어나며, 이 전극을 산화전극(anode)라고 부른다. 이때 방전이란 전지가 갖고 있는 화학 에너지를 전기에너지로 변환시키는 과정을 의미한다.
- 양극에서는 전지의 방전동안 외부회로를 통해 음극으로부터 전달된 전자에 의해 전극 물질의 환원반응(reduction, \(B^+ + e^- → B \))이 일어나며, 이 전극을 환원전극(cathode)라고 부른다.
- 전해질(electrolyte)은 두 전극 사이에서 이온을 전달하는 이온 전도체(ionic conductor)로서, 전자에 대한 전도성은 없으며 단지 이온전도성 만을 나타낸다.
- 2차전지는 산화, 환원반응이 가역적이며, 반복적 사용이 가능하다.
- 2차전지 전극에서는 산화뿐만 아니라 환원 반응도 일어날 수 있으므로 방전 시 산화전극의 역할을 하던 전극은 충전시 환원전극으로 전환된다. 따라서 전극의 정의는 방전동안 산화전극을 음극, 환원전극을 양극이라 하고 충전 동안에도 그 정의는 변하지 않는다. 이는 이차전지 전극의 정의가 방전 과정을 기준으로 하기 때문이다.
완전 셀(full cell)과 반쪽 셀(half cell)
- 완전셀 : 양극과 음극이 동시에 전기화학 반응에 참여하는 완전한 전지의 형태
- 반쪽셀 : 환원전극 혹은 산화전극 중 한쪽 전극만 작업전극으로 하고, 상대전극을 기준전극으로 사용하기 때문에 작업전극에서만 일어나는 현상을 측정하고 분석하기가 용이하며 전극 소재들의 기본 성질을 규명하는데 유리하다
전기화학 반응과 전위
- 방전 시 전지에서의 전기화학적 반응은 전지가 생산해낼 수 있는 전기적 에너지와 상관관계를 가진다.
\[(2.1)\quad pA+qB=rC+sD \]
- p,q,r,s : 각 화학종에 대한 각각의 양론계수(stoichiometric coefficient)이다. 위 반응식에 관한 Gibbs 자유에너지 변화를 활동도 a에 관한 식으로 표현가능
\[(2.2)\quad \triangle G=\triangle G^O+RT\ln(a^r_C a^s_D / a^p_A a^q_B) \]
- 전지가 평형상태에서 얻을 수 있는 일은 최대의 일에 해당하며, 이는 전기화학 반응동안 Gibbs 자유에너지의 변화 \(\triangle G\)로 나타낼 수 있다
\[(2.3)\quad W_{rev} = W_{max} \quad \\(2.4) -W_{max}=\triangle G\]
- 전기적 에너지는 전지 내를 흐르는 전하 Q 및 전위차 E와 다음과 같은 관계가 있다.
\[(2.5)\quad -W_{max}=QE\]
- Q는 전지 내 전자의 갯수와 전하량(e)의 곱으로 나타낼 수 있다. 전자 갯수 \(n_e\) 는 전자의 몰 수와 아보가드로 수의 곱에 해당한다.
\[ (2.6)\quad Q=n_e e\\(2.7)\quad Q=n N_Ae \\ (2.8)\quad Q=nF \]
- F는 Faraday 상수로서, 전자 1몰에 해당하는 전하량(96,485 C/mol)이다. 따라서 두 전극이 서로 다른 전위를 갖는다면 그 전위차로 인해 n 몰의 전자가 이동할 때 전지가 행하는 전기적 일은 다음식으로 표시된다.
\[(2.9)\quad W_{max}=nFE=-\triangle G\]
- 전기화학 반응에 참가하는 반응물과 생성물들이 모두 표준상태인 경우에 전지의 전위는 표준전위 \(E^o\)로 나타낸다.
\[(2.10)\quad \triangle G^o=-nFE^o\]
- (2.2) & (2.10)으로부터 Nernst 식이 얻어지고 전위차는 전기 화학 반응에 참여하는 성분들의 농도에 의해 영향을 받는다.
\[ (2.12)\quad E=E^o-RT/nF \ln(a^r_C a^s_D/a^p_A a^q_B) \]
2-2 전지의 전압과 전류
전압
전기 회로에 있는 두 지점간 전위의 차이, 전기를 흐르게 하는 원동력으로서 기전력(electromotive force)라고도 부른다.
실제 전지전압은 구동하는 조건(온도, 압력 등)에 영향을 받으므로 표준 상태인 1기압, \(25^oC\), 1몰의 수소농도 이며 평형상태하에서의 전위를 표준전극전위(standard electrode potential)로 정한다.
\[(2.13)\quad E_{rxn} = E_{right}-E_{left} \]
- 자발적 산화환원반응을 가지는 galvanic cell인 경우 \(E{rxn}\)는 양의 전압값인 반면, 전기화학 반응이 비자발적인 경우 \(E{rxn}\)는 음의 전압값을 가지는 electrolytic cell에 해당한다.
- 전자는 평형 상태(전류가 거의 흐르지 않는 상태)인 경우에만 전지내 반응의 \(\triangle G\)와 같은 크기의 전기적 에너지를 공급할 수 있다. 그러나 실직적으로 방전 반응시의 전지에서는 전류가 흐르는 상태로서 열역학적으로 비평형상태 하에서 진행된다고 볼 수 있다.
- 이러한 방전과정에서 전압은 개방회로전압(OCV)보다 항상 작은 값을 나태내므로 열역학적으로 가능한 최대 에너지를 이용할 수 없게 된다.
- 여기서 OCV보다 실제 전압이 낮아지는 이유는 전지 내부의 저항 및 전극/전해질 계면에서의 전하 이동과 관련된 분극(polarization)현상과 관련지어 설명할 수 있다.
- 반면, 역방향인 충전 과정에서 전압은 OCV보다 높은데, 그 이유는 내부저항 및 활성화 분극에 따른 과전압의 형성과, 이온전도가 전자전도보다 낮으며, 전극 재료에 불슨물이 포함될 수 있고, 전극재료 표면과 내부에서의 리튬이온 확산 속도의 차이로 전극의 부위별 리튬이온 농도 차이가 유발되어 분극현상을 일으키기 때문이다.
전류
단위 시간당 전하의 이동량
전극에서의 전기화학 반응속도와 밀접한 관계를 가진다.
전극반응의 속도는 전해질에서 전극으로의 물질전달, 전극 활물질 표면에서의 전자전달 반응 등에 의해 결정된다.
가역반응을 나타내는 반응물 O, 생성물 R
\[(2.14)\quad O+ne <⇒R\\(2.15)\quad v_f=k_f C_o(0,t)=\frac{i_c}{nFA} \\(2.16)\quad v_b=k_bC_R(0,t)=\frac{i_a}{nFA}\]
\[ v_f, v_b : 전극에서의\ 정반응\ 및\ 역반응의\ 반응속도 \\k_f, k_b : 각\ 반응의\ 속도상수\\C_o, C_R: 산화성분\ 및\ 환원성분의\ 농도\\C_o(x,t): 시간\ t\ 및\ 전극표면으로부터의\ 거리x에서의\ 산화성분\ 농도\\i_c,i_o: 환원\ 및\ 산화에\ 관한\ 전류\\n,F,A: 반응에\ 기여하는\ 전자의\ 몰수,\ Faraday\ 상수,\ 전극의\ 표면적 \]
- 전극에서의 순수 반응속도
\[ v_{net}=v_f-v_b=k_fC_o(0,t)-k_bC_R(0,t)=\frac{i}{nFA} \]
⇒ 전극에서 생성되는 전류는 순수 반응속도에 의해 크게 영향을 받는다. 만약 전극에서의 반응이 평형상태에 이르게 되면 정반응 속도 및 역반응 속도가 동일하게 됨으로써 순수 반응속도는 0이 되어 전류의 생성이 중지된다.
분극
전극전위 값이 평형상태에서 과하거나 부족하게 되는 현상
전지 내부 반응이 진행될 때, 각 요소의 전하 이동과정이 같은 속도로 일어나지 않으므로 어느 특정 과정의 전하이동과정이 상대적으로 늦어지는 경우, 전지의 전체 반응에 대한 속도제한과정(rate limiting process)이 된다.
따라서 양 단자 사이에 전류가 흐르게 되면 전압 E는 항상 평형전압보다 크거나(충전) 작게(방전) 나타난다. 이때 그 차이를 과전압(overpotential)이라고 한다.
\[ η=E-E_{eq}\]
2-3 전지의 특성
용량(Capacity)
- 주어진 방전 조건하에서 전지를 완전히 방전시켰을 때 얻을 수 있는 전하량, 전류와 시간의 곱. 전지의 이론용량은 전지의 활물질의 양에 의해 결정됨
\[(2.19)\quad C_T=xF \]
→ x: 전지가 완전히 방전되는 동안 반응으로부터 생성되는 전자의몰 수
- 일반적 전지의 충방전 속도를 표시할 때, C rate 를 자주 사용한다. 전지 용량과 충방전 전류 사이에는 다음과 같은 관계가 주어진다
\[(2.20)\quad h=C_p / i \]
→ h: 용량을 완전히 충방전하는데 걸리는 시간, i: 충방전 전류, \(C_p\): 전지의 용량
⇒ h의 역수 : C rate, C값이 클수록 충전 또는 방전을 시키는데 소요되는 시간이 짧아지는 것
- 전지나 전극의 용량을 나타낼 때에는 전극 단위 무게당 용량이나, 단위 부피당 용량을 사용하여 서로 비교하기가 용이해진다.
에너지 밀도
- 단위 무게나 부피로부터 얻어질 수 있는 에너지
\[(2.21)\quad \triangle G=-FE=\varepsilon_T \]
→ E: 전지의 기전력 \(\varepsilon\): 1몰의 전지 반응에 대한 이론적 에너지
- 1 몰의 반응물로부터 얻을 수 있는 실제의 에너지 \(\varepsilon_p \)
\[ (2.22)\quad \varepsilon_p = \int Edq=\int(E_i)dt=-F(E_{eq}-\eta)\]
→ 전지의 방전 속도, 즉 단위 시간당 방전 전류가 증가함에 따라 전지의 전압은 점차 평형 전압으로부터 벗어나게 된다.
출력
- 단위시간 당 생산할 수. 있는 에너지
\[(2.23)\quad P(W)=i(A)\cdot E(V)\]
전지의 출력은 주어진 전압에서 얼마나 큰 전류를 흘려줄 수 있는가에 대한 척도가 된다.
일반적으로 전류가 증가할 때 전지로부터 얻을 수 있는 출력은 초기에는 증가하다가 최고 값에 도달한 후 감소하는 경향을 보임 → 분극현상과 관련
→ 전류가 특정 값 이상으로 증가하면 전지 전압이 감소하기 때문에 주어진 전압 범위에서 얻을 수 있는 용량도 감소
- 이런 분극현상은 리튬이온의 확산속도 및 전지 내부저항과 관련되므로 이온의 확산속도 및 전기 전도도 특성을 향상 시키는 것이 필요하다.
충방전 수명(cycle life)
- 일정 용량 이상의 성능을 구현할 수 있는 전지의 충,방전 횟수
- 반복되는 충,방전 과정에서의 양극 및 음극 활물질의 구조 안정성에 크게 좌우됨
- 비가역 용량 : 방전 과정동안 이미 충전된 전하량 중에서 방전되지 못한 전하량 → 전극과 전해질 계면에 형성되는 새로운 층(layer)에 의해 야기됨
- N회 충,방전 사이클 진행 후 용량 유지율은 \(C_N/C_1(%)\)로 주어지며, 상대적인 용량 감소는 \(C_1- C_N)/C_1 \)으로 나타난다.
- 일반적으로 충,방전 수명은 방전 깊이에 의해 영향 받으며, 리튬이차전지에서는 얕은 방전(low depth of discharge)상태에서 충전이 반복될 때, 즉 용량을 완전히 소모하기 전에 방전을 끝내고 다시 충전시킬 때 더 긴 충,방전 수명을 나타낸다.
방전 곡선 (discharge curves)
- 방전 조건 : 일정 전류, 일정 출력, 일정 외부저항
- 측정 성질 : 전지전압, 전류, 출력
- 측정 변수 : 방전시간, 용량, 리튬이온 점유율
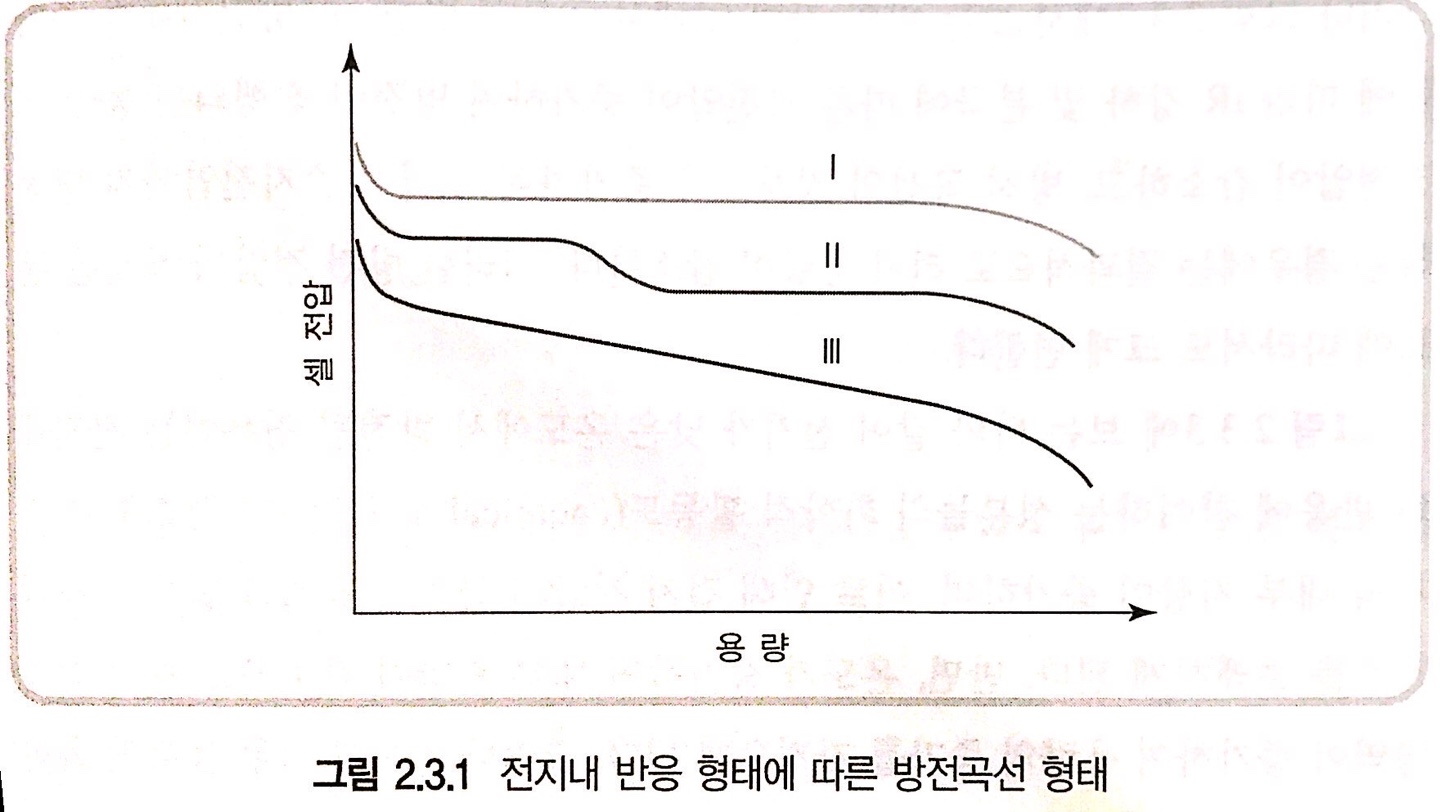
< 그림 1 >
전류의 인가시간에 따른 전압의 변화
- 1: 방전이 진행되는 동안 전지내의 반응이 전지전압에 거의 영향을 끼치지 않는 경우
- 2: 방전이 진행되는 동안 전지내의 반응 메커니즘이 변화되어 2개의 평탄 영역을 나타내는 경우
- 3: 방전이 진행되는 동안 반응물질과 생성물질의 조성 및 전지의 내부저항등이 계속 변화하는 경우
\[ E_{cell}=E_{cell}^o -(nRT/F)\ln(y/1-y)+ky\]
y: 리튬이온 점유율, ky: intercalation된 리튬이온 사이의 상호작용이 전지 전압에 미치는 영향
- 이때 전지 전압의 기울기 변화는 전극에서의 리튬이온 확산속도, 상전이, 결정구조 변화 및 용해 등 직접적인 요인과, 양극 활물질의 입자 크기 및 성분, 온도, 전해질 특성, 분리막의 기공 등 추가적인 요인에 따라 y, k 값이 변화될 수 있다.
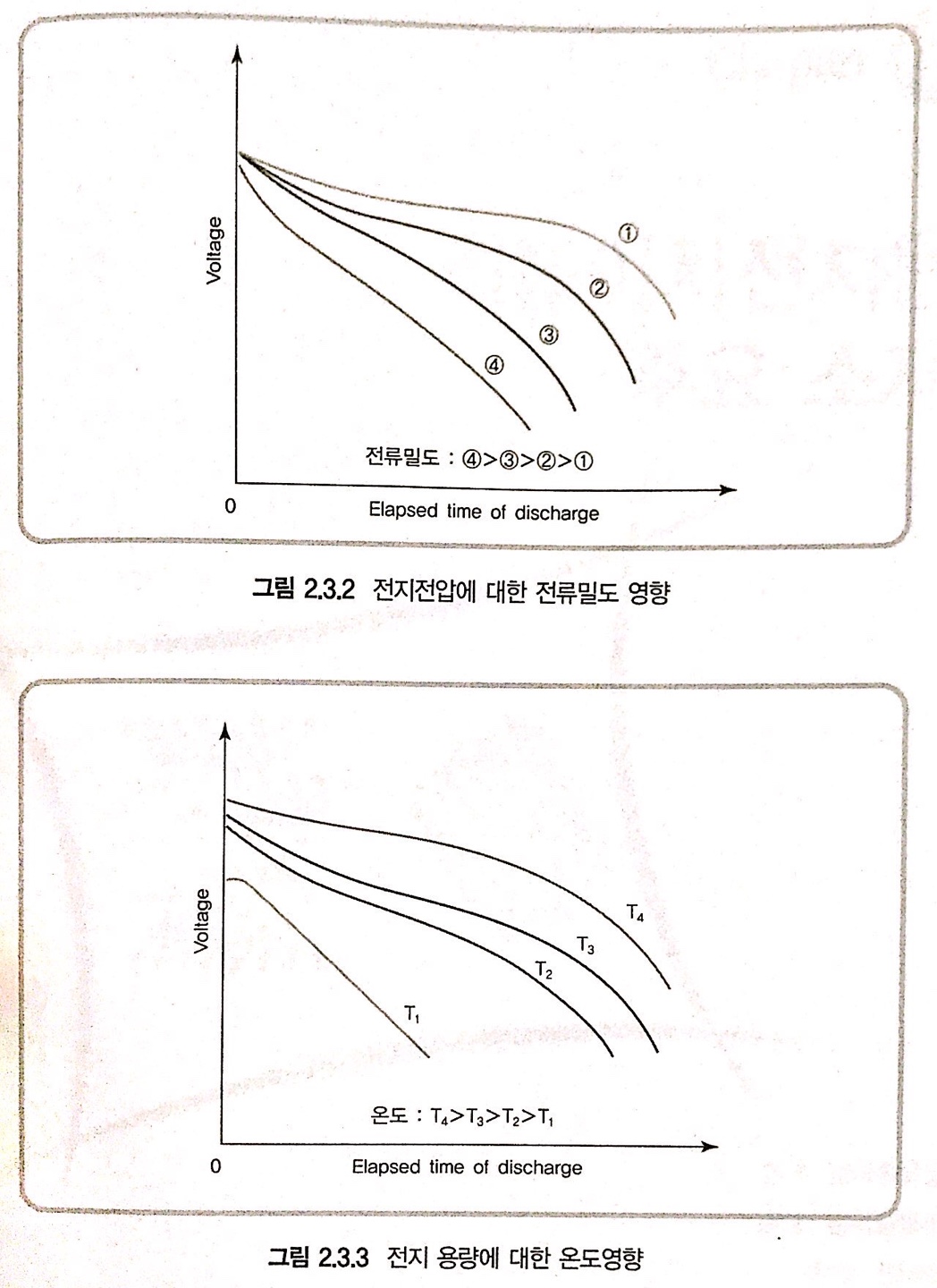
< 그림 2 >
- 전지가 방전 과정에서 전류 밀도가 매우 낮은 경우 작동 전지의 전압은 이론적 평형 전압에 근접하며 방전용량 또한 이론 용량에 가깝다
- 1→4, 방전 전류가 증가함에 따라 iR 강하 및 분극에 따른 과전압이 증가하여 방전이 진행되는 동안 전지 전압이 감소하고, 방전 곡선의 경사도가 증가하여 주어진 종지 전압까지 방전하는 경우에는 결과적으로 전지 용량이 감소한다. 이런 특성은 온도에 따라서도 크게 변한다.
< 그림 3 >
- 낮은 온도에서 방전될 경우, 전지내의 반응에 참여하는 성분들의 화학적 활동도가 감소하여 전지 내부저항이 증가하며, 전지 전압의 급격한 강하와 함께 용량 감소
- 높은 온도에서는 내부 저항이 감소하고 방전 전압영역이 증가하여 용량의 증가를 가져오나 화학적 활동도가 증가하여 자가 방전을 포함한 원하지 않은 종류의 부가적인 화학적 반응 을 일으킬 수 있다