Chap3. Mechanical Properties of Materials
모든 방향에 힘이 같다는 등방성 가정!!
Force - Displacement Curve
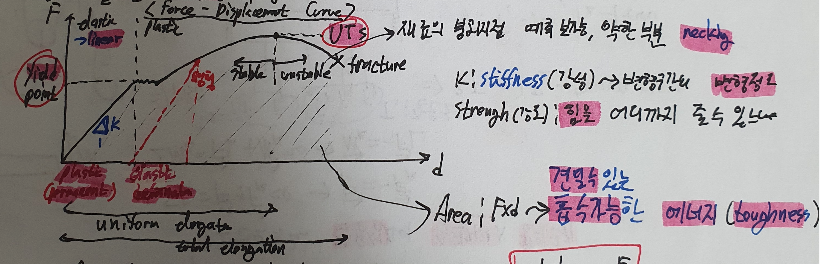
- fracture : 재료의 붕괴 시점 ⇒ 예측 불가능
- UTS를 지나면 약한 부분이 necking
- K : stiffness(강성) → 변형 구간의 변형정도
- strength(강도) → 힘을 얼마나 줄 수 있느냐
- Area = F x d : 흡수 가능한 (견딜 수 있는) 에너지 (toughness)
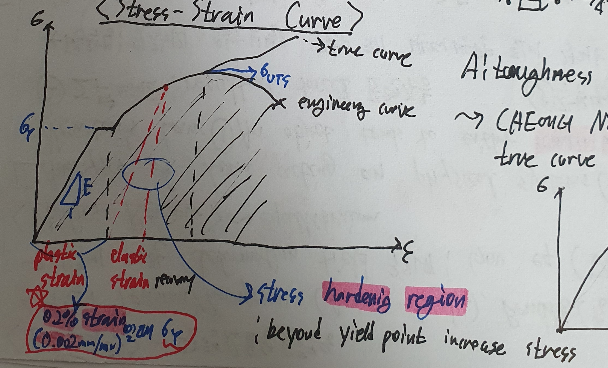
- work(strain) hardening : 소성영역에서 더 강해짐 / 에너지 흡수 등력이 줄어들음
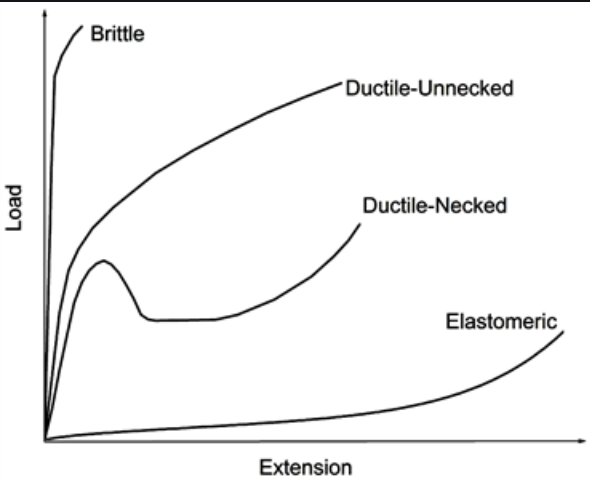
ductile : large plastic deformation, metal, energy absorption (소성변형 시)
brittle : almost no plastic deformation(\(yield\ point \approx\ fracture\) ), high yield stress, not goot to absorb energy, rock, plastic, carbon
elastomer : very long elongation, energy absorption (potential), rubber
→ 재료의 temp 상승 : E, strength 감소 / 연신율 증가
소재에 저장되는 에너지 : 탄성변형까지!
Hooke's Law : \(σ = E\varepsilon\) ⇒ 탄성 영역에서만!
modulus of resilience : permanent damage 없이 E 흡수
modulus of toughness : fracture 까지 E 흡수
Poisson ratio : 줄어드는 폭의 역학적 비율, 탄성 영역까지만 적용됨
\[ \varepsilon_{zz}=\frac{L-L_0}{L_0}, \varepsilon_{xx}=\frac{w-w_0}{w_0},\varepsilon_{yy}=\frac{D-D_0}{D_0}\\ \nu_{yy}=-\frac{\varepsilon_{yy}}{\varepsilon_{zz}},\quad \nu_{xx}=-\frac{\varepsilon_{xx}}{\varepsilon_{zz}} \]
→ 금속 : 0.3, 고무 : 0.5
- Shear stress \(\tau=Gγ,\quad G=\frac{E}{2(1+\nu)},\quad γ=\frac{\rho}{L}\phi \)
Strain-stress relation
- elastic에서만 적용, 등방성
- 3D
\[\left(\begin{array}{c}\sigma_{xx}\\ \sigma_{yy}\\\sigma_{zz}\\\sigma_{yz}\\\sigma_{xz}\\\sigma_{xy}\end{array}\right)=\frac{E}{(1+\nu)(1-2\nu)}\left(\begin{array}{c}1-\nu & \nu & \nu & 0 &0&0\\ &1-\nu&\nu&0&0&0\\&&1-\nu&0&0&0\\&&&\frac{(1-2\nu)}{2}&0&0\\&SYM&&&\frac{(1-2\nu)}{2}&0\\&&&&&\frac{(1-2\nu)}{2}\end{array}\right)\left(\begin{array}{c}\varepsilon_{xx}\\ \varepsilon_{yy}\\\varepsilon_{zz}\\2\varepsilon_{yz}\\2\varepsilon_{xz}\\2\varepsilon_{xy}\end{array}\right)\]
\[\left(\begin{array}{c}\varepsilon_{xx}\\ \varepsilon_{yy}\\\varepsilon_{zz}\\\varepsilon_{yz}\\\varepsilon_{xz}\\\varepsilon_{xy}\end{array}\right)=\frac{1}{E}\left(\begin{array}{c}1 & -\nu & -\nu & 0 &0&0\\ &1&-\nu&0&0&0\\&&1&0&0&0\\&&&2(1+\nu)&0&0\\&SYM&&&2(1+\nu)&0\\&&&&&2(1+\nu)\end{array}\right)\left(\begin{array}{c}\sigma_{xx}\\ \sigma_{yy}\\\sigma_{zz}\\2\sigma_{yz}\\2\sigma_{xz}\\2\sigma_{xy}\end{array}\right)\]
2D
- Plane Stress : 두께가 면적에 비해 너무 작으면 힘을 만들지 못함 \(σ{zz}=σ{xz}=σ_{yz}=0\)
\[\left(\begin{array}{c}\sigma_{xx}\\ \sigma_{yy}\\\sigma_{xy}\end{array}\right)=\frac{E}{1-\nu^2}\left(\begin{array}{c}1&\nu&0\\ &1&0\\SYM&&1-\nu\end{array}\right)\left(\begin{array}{c}\varepsilon_{xx}\\ \varepsilon_{yy}\\\varepsilon_{xy}\end{array}\right),\quad σ_{zz}=\frac{P}{A_z\rightarrow \infty}\]
- Plane strain : 면적에 비해 두께가 큼
\[\varepsilon_{zz}=\frac{u_z = 0}{L_0\rightarrow\infty} \left(\begin{array}{c}\sigma_{xx}\\ \sigma_{yy}\\\sigma_{xy}\end{array}\right)=\frac{E}{(1+\nu)(1-2\nu)}\left(\begin{array}{c}1-\nu&\nu&0\\ &1-\nu&0\\SYM&&1-2\nu\end{array}\right)\left(\begin{array}{c}\varepsilon_{xx}\\ \varepsilon_{yy}\\\varepsilon_{xy}\end{array}\right)\]