Chap4&5. Axial Load & Torsion
Chap 4. Torsion
- Saint Vernant Principle : stress concentration이 먼 곳에서는 beam 내부의 stress distribution이 uniform 하다고 가정
→ 응력 집중의 효과는 국부적이므로 힘의 원인에서 충분히 떨어진 고셍서는 응력이 균일하다고 볼 수 있다.
Equilibrium equation : \(σ A(x)=N(x)\)
Stress Strain equation : \(σ{xx}=E\varepsilon{xx} ⇒ E\frac{\partial u}{\partial x}A(x)=N(x)\)
Strain-Displacement equation : \(\varepsilon_{xx}=\frac{\partial u_{xx}}{\partial x}\)
\[\frac{\partial u}{\partial x}=\frac{N(x)}{EA(x)} → u=\int \frac{N(x)}{EA(x)}dx \]
- Boundary Condition : reaction force를 주는 것 ⇒ 움직일 수 있으면 reaction force가 없다
Chapter 5. Torsion
- Twisting : 힘은 무조건 쌍으로 나온다, 토크는 상대적 관점, 토크 들의 방향이 반대여야 twist 생김 → Shear deformation
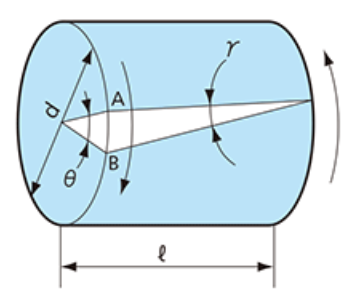
- γ : 각도의 변화 → \(d=Lγ\) : 각도는 같지만 x 따라서 회전량은 다름
\[ \rho = \frac{d}{2},\quad d=\rho\phi ⇒ Lγ=\rho\phi\\\therefore γ=\frac{\rho}{L}\phi, \quad\tau=Gγ \\ \tau=\frac{T\cdot c}{J=\int r^2dA},\ \phi=\frac{TL}{GJ}\]
- Thin wall Twisting
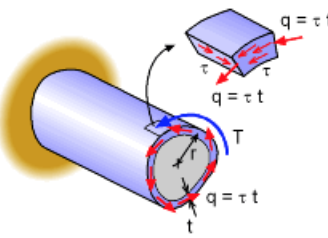
\[ \tau \cdot t=q[N\cdot m]:const.\\T=\oint q\cdot hds=q\oint hds ,\quad \frac{h \cdot ds}{2}=A_m\\ ⇒ T=2q\int bA_m,\ q=\tau t → 2\tau \cdot t\int dA_m → \tau=\frac{T}{2tA_m}\]