Chap10. Moment of Inertia
Objectives
- To develop a method ofr determining the moment of inertia for an area.
- To introduce the product of inertia and show how to determine the maximum and minimum moments of inertia for an area
- To discuss the mass moment of inertia
10.1 Definition of Moments of Inertia for Areas
- Whenever a distributed loading acts perpendicular to an area and its intensity varies linearly, the computation of the moment of the loading distribution about an axis will involve a quantity called teh moment of inertia of the area.
(1) Moment of Inertia
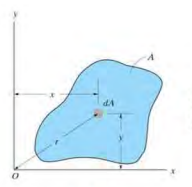
\[I_x = \int_A y^2 dA, \quad I_y = \int_A x^2 dA, \quad J_O = \int_A r^2 dA = I_x + I_y\]
10.2 Parallel-Axis Theorem for an Area
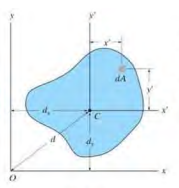
\[I_x = \int_A (y'+d_y)^2 dA = \int_A y'^2 dA + 2d_y \int_A y'dA + d^2_y\int_A dA = \bar{I}_{x'} + Ad^2_y, \\ I_y = \bar{I}_{y'} + Ad^2_x, \quad J_O = \bar{J}_C + Ad^2\]
10.3 Radius of Gyration of an Area
- used for the design of columns in structural mechanics
\[k_x = \sqrt{\frac{I_x}{A}}, \quad k_y = \sqrt{\frac{I_y}{A}}, \quad k_O = \sqrt{\frac{J_O}{A}}\]
10.5 Product of Inertia for an Area
\[I_{xy} = \int_A xydA\]
(1) Parallel-Axis Theorem
\[I_{xy} = \int_A (x'+d_x)(y'+d_y)dA = \int_A x'y'dA + d_s\int_A y'dA + d_y\int_A x'dA + d_x d_y \int_A dA = \bar{I}_{x'y'} + Ad_x d_y\]
10.6 Moments of Inertia for and Area about inclined Axes
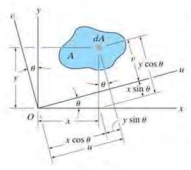
\[u=xcos\theta + ysin\theta, \quad v = ycos\theta - xsin\theta \\ dI_u = v^2dA = (ycos\theta - xsin\theta)^2dA, \quad dI_v = u^2dA = (xcos\theta + ysin\theta)^2dA, \quad dI_{uv} = uvdA = (xcos\theta + ysin\theta)(ycos\theta - xsin\theta)dA \\ I_u = I_x cos^2\theta + I_y sin^2\theta - 2I_{xy}sin\theta cos\theta, \quad I_v = I_x sin^2\theta + I_y cos^2\theta - 2I_{xy}sin\theta cos\theta, \quad I_{uv} = I_x sin\theta cos\theta + I_y cos\theta sin\theta - I_{xy}(cos^2\theta - sin^2\theta) \\ I_u = \frac{I_x + I_y}{2} + \frac{I_x - I_y}{2}cos2\theta - I_{xy}sin2\theta, \quad I_v = \frac{I_x + I_y}{2} - \frac{I_x - I_y}{2}cos2\theta + I_{xy}sin2\theta, \quad I_{uv} = \frac{I_x - I_y}{2}sin2\theta + I_{xy}cos2θ\]
(1) Principal Moments of Inertia
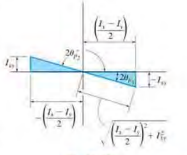
\[\frac{dI_i}{d\theta} = -2(\frac{I_x - I_y}{2})sin2\theta - 2I_{xy}cos2\theta=0 \\ tan2\theta_p = \frac{-I_{xy}}{(I_x - I_y)/2} \\ I_{max,\ min} = \frac{I_x+I_y}{2} \pm \sqrt{(\frac{I_x - I_y}{2})^2 + I_{xy}^2}\]
10.7 Mohr's Circle for Moments of Inertia
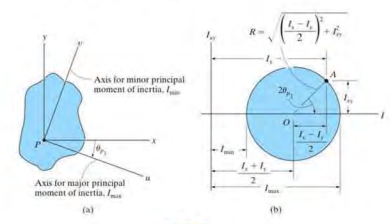
10.8 Mass Moment of Inertia
$