Chap11. Virtual Work
Objectives
To introduce the principle of virtual work and show how it applies to finding the equilibrium configuration of a system of pin-connected members
To establish the potential-energy function and use the potential-energy method to investigate the type of equilibirum ofr stablity of a rigid body or system of pin-connected members
11.1 Definition of Work
(1) Work of Force
- A force does work when it undergoes a displacement in the direction of its line of action
\[dU = F dr cos\theta = F \cdot dr\]
- 1[J] = 1[\(N\cdot m\)]
(2) Work of a Couple Moment
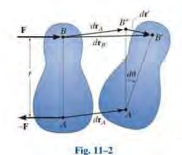
- \(U = Fdr'' = Frd\theta => dU = Mdθ\)
(3) Virtual Work
\[\delta U = F cos\theta \delta r = M \delta θ\]
11.2 Principle of Virtual Work
- If a body is in equilibrium, the algebraic sum of the virtual work done by all the forces and couple moments acting on the body is zero for any virtual displacement of the body.
\[\delta U =0\]
- No added advantages is gained by solving particle and rigid-body euqilibirum problems using the principle of virtual work because the virtual displacement factors out, leaving the euqation that could have been obtained in a more direct manner by simply applying an equation of equilibrium.
11.4 Conservative Forces
- Conservative Forces : when the work of a force only depends upon its initial and final positions, and is indenpendent of the path it travels.
(1) Weight
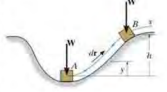
\[dU = W\cdot dr =-W(dr cos\theta)=-Wdy ,\quad U=-\int^h_0 Wdy=-Wh\]
- it only depends on height, and is independent of the path along which it travels
(2) Spring Force
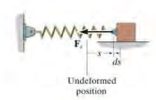
\[dU=-F_s ds = -ksds ,\quad U=\int^{s_2}_{s_1} ksds = -(\frac{1}{2}ks^2_2 -\frac{1}{2}ks^2_1)\]
(3) Friction : the frictional force depends on the path. It is nonconservative, and most of the work is dissipated from the body in the form of heat
11.5 Potential Energy
- Potential Energy : The capacity ot work, depends on the location of the body relative to a fixed reference position or datum
(1) Gravitational Potential Energy : when a body is located a distance y above a fixed horizontal reference \(V_g = Wy\)
(2) Elastic Potential Energy : when a spring is eigher elongated or compressed by an amount x from its unstreched position, energy stored in the spring \(V_e= \frac{1}{2} ks^2\)
(3) Potential Function \(V = V_g + V_e\)
11.6 Potential-Energy Criterion for Equilibrium
\(dU = V(q) - V(q+dq)=-dV\) , since the principle of virtual work \(\delta U = 0 => \frac{dV}{dq}=0\)
- When a frictionless connected system of rigid bodies is in equilibrium, the first derivative of its potential function is zero.
11.7 Stability of Equilibirum Configuration
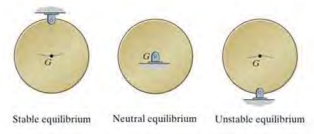
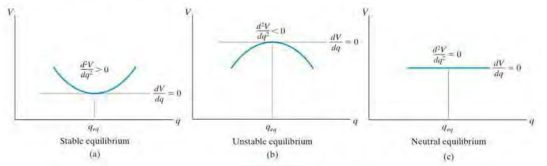
(1) Stable Equilibrium
- when a system has a tendency to return to its original position when a small displacement is given to the system
- The potential energy of the system is at its minimum
(2) Neutral Equilibrium
- when the system still remains in equilibrium when the system is given a small displacement away from its original position.
- The potential energy of the system is constant
(3) Unstable Equilibrium
- when a system has a tendency to be displaced further away from its original equilibrium position when it is given a small displacement
- The potential energy is a maximum