Chap2 Force Vectors
Objectives
- To show how to add forces and resolve them into components using the Parallelogram Law
- To express force and position in Cartesian vector form and explain how to determine the vector's magnitude and direction
- To introduce the dot product in order to determine the angle between two vectors or the projection of one vector onto another
2.1 Scalars and Vector
(1) Scalar : a positive or negative physical quantity that can be completely specified by its magnitude
(2) Vector : a physical quantity that requires both a magnitude and a direction
2.2 Vector Operations
(1) Multiplication and Division of a Vector by a Scalar : magnitude changes
(2) Vector Addition : parallelogram law of addition
- Parallelogram Law
● Two component forces add according to the parallelogram law, yielding a resultant force that forms the diagonal of the parallelogram
● If a force is to be resolved into components along two axes u and v, then start at the head of force F and construct lines parallel to the axes, thereby forming the parallelogram.
● Label all the known and unknown force magnitudes and the angles on the sketch and identify the two unknowns as magnitude and direction.
(3) Vector Subtraction : adds the fliped vector
2.5 Cartesian Vectors
(1) Cartesian Representation : \(A = A_x \hat{i} + A_y \hat{j} + A_z \hat{k}\)
(2) Magnitude of a Cartesian Vector : \(A = \sqrt{A^2_x + A^2_y + A^2_z}\)
- The magnidute is equal to the positive square root the sum of the squares of its components
(3) Direction of a Cartesian Vector
Coordinate direction angles \(\alpha, \beta, γ\)
direction cosines : \(cos\alpha = \frac{A_x}{A} \quad cos\beta = \frac{A_y}{A} \quad cos\gamma = \frac{A_z}{A}\)
\[u_A = \frac{\overrightarrow{A}}{A} = \frac{A_x}{A}\hat{i} + \frac{A_y}{A}\hat{k} + \frac{A_z}{A}\hat{k} \\ cos^2\alpha + cos^2\beta + cos^2\gamma = 1\]
2.7 Position Vectors
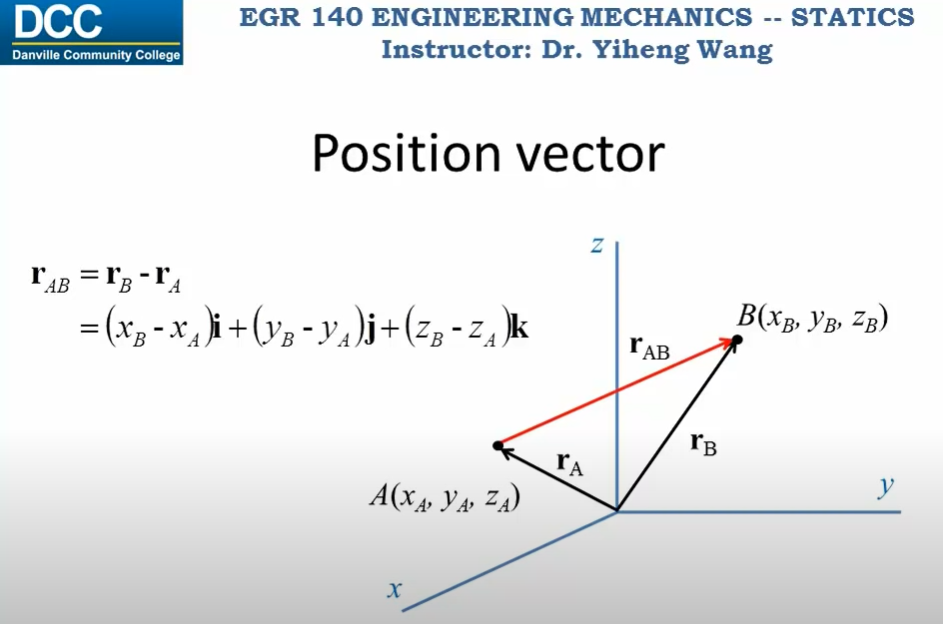
- Components of the position vector is formed by taking the coordinates of the tail of the vector A and subracting them from the corresponding corrdinates of the vector B
\[\hat{r} = \hat{r_B} - \hat{r_A} = (x_B - x_A)\hat{i} + (y_B - y_A)\hat{j} + (z_B - z_A)\hat{k}\]
2.8 Force Vector Directed Along a line
- When the direction of a force is specified by two points through which its line of action passes.
\[F\bf = F\it u = F\it \frac{r\bf}{r\it} = F\it (\frac{(x_B - x_A)\hat{i} + (y_B - y_A)\hat{j} + (z_B - z_A)\hat{k}}{\sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2}}) \\ F\bf :\ units\ of\ force\]
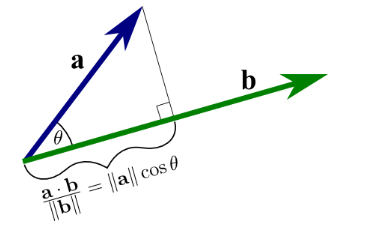
2.9 Dot Product
- a particular method for "multiplying" two vectors $ A \cdot B = ABcos\theta $, resulting a scalar
(1) Laws of Operation
- Commutative law : \( A \cdot B = B \cdot A \)
- Multiplication by a scalar: \(a(A \cdot B) = (aA) \cdot B = A \cdot (aB)\)
- Distributed Law : \(A \cdot (B+D) = (A \cdot B) + (A \cdot D) \)
(2) Cartesian Vector Formulation
\[A\ \cdot\ B\ =\ (A_x \hat{i} + A_y \hat{k} + A_z \hat{k})\ \cdot\ (B_x \hat{i} + B_y \hat{k} + B_z \hat{k})\ \\=\ A_x B_x(\hat{i}\ \cdot\ \hat{i})\ +\ A_x B_y(\hat{i}\ \cdot\ \hat{j})\ +\ A_x B_z(\hat{i}\ \cdot\ \hat{k})\ \\+\ A_y B_x(\hat{j}\ \cdot\ \hat{i})\ +\ A_y B_y(\hat{j}\ \cdot\ \hat{j})\ +\ A_y B_z(\hat{j}\ \cdot\ \hat{k})\ \\+\ A_z B_x(\hat{k}\ \cdot\ \hat{i})\ +\ A_z B_y(\hat{k}\ \cdot\ \hat{j})\ +\ A_z B_z(\hat{k}\ \cdot\ \hat{k})\ =\ A_x B_x + A_y B_y + A_z B_z\]
(3) Applications
a. The angle formed between two vectors or intersecting lines
\[\theta = cos^{-1}(\frac{A\bf\ \cdot\ B\bf}{AB}), \quad 0^o \leq \theta \leq 180^o\]
=> If two line are perpendicular, \(A\cdot B = 0 \)
b. The component of a vector parallel and perpendicular to a line : \(A_a = Acos\theta = A\cdot u_a\)