Chap4. Force System Resultants
Objectives
- To discuss the concept of the moment of a force and show how to calculate it in two and three dimensions
- To provide a method for finding the moment of a force about a specified axis
- To define the moment of a couple
- To present methods for determining the resultants of nonconcurrent force systems
- To indicate how to reduce a simple distributed loading to a resultant force having a specified location
4.1 Moment of a Force - Scalar Formulation
(1) torque(moment) : a tendency for the body to rotate about a poin that is not on the line of action of the force
a. magnitude of moment is directly proportional to the magnitude of the force and the perpendicular distance or moment arm d.
b. moment is a vector quantity
(2) Magnitude \(M_O = Fd\)
- d is the moment arm or perpendicular distance from the axis at origin point to the line of action of the force
(3) Direction : defined by its moment axis, which is perpendicular to the plane that contains the force and its moment arm with the Right-hand rule
(4) Resultant Moment : the resultant moment(\(M_R\) about a point can be determined by finding the algebraic sum of the moments caused by all the forces in the system. positive moments are counterclockwise.
4.2 Cross Product
\[C = A \times B\]
(1) Magnitude : the product of the magnitudes of A and B the sine of the angle $\theta$ between their tails
\[C = ABsinθ\]
(2) Direction : perpendicular to the plane containing A and such that C is specified by the Right-hand rule.
\[C=A\times B=(ABsine\theta)u_C\]
(3) Laws of Operation
\[A \times B = - B \times A\]
\(a(A\times B) = (aA) \times B = A \times (aB) = (A\times B)a\) , the magnitude of the resultant vector and its direction are the same in each case
\[A \times (B+D) = (A\times B)+(A\times D)\]
(4) Cartesian Vector Formulation
\(A \times B = (A_x \hat{i} + A_y \hat{j} + A_z \hat{k}) \times (B_x \hat{i} + B_y \hat{j} + B_z \hat{k}) \= (A_x B_x (\hat{i} \times \hat{i})) +(A_x B_y (\hat{i} \times \hat{j})) + (A_x B_z (\hat{i} \times \hat{k})) + (A_y B_x (\hat{j} \times \hat{i})) \+ (A_y B_y (\hat{j} \times \hat{j})) + (A_y B_z (\hat{j} \times \hat{k})) + (A_z B_x (\hat{k} \times \hat{i})) + (A_z B_y (\hat{k} \times \hat{j})) \+ (A_k B_k (\hat{k} \times \hat{k})) = (A_y B_z - A_z B_y)\hat{i} - (A_x B_z - A_z B_x)\hat{j} + (A_x B_y - A_y B_x)\hat{k}
\left|
\begin {array}{lcr}
\hat{i} & \hat{j} & \hat{k}
A_x & A_y & A_z
B_x & B_y & B_z
\end{array}
\right|\)
4.3 Moment of a Force - Vector Formulation
\[M_O = r \times F\]
- r represents a position vector directed from O to any point on the line of action of F
(1) Magnitude \(M_O = rFsin\theta = F(rsin\theta) = Fd\)
(2) Direction : Right-hand rule, sliding r to the dashed position and curling the right-hand fingers from r toward F
(3) Principle of Transmissibility : we can use any position vector r measured from point O to any point on the line of action of the force F. \(M_O = r_1 \times F = r_2 \times F = r_3 \times F\)
(4) Resultant Moment of a System of Forces \(M_R = \sum (r \times F)\)
4.4 Principle of Moments
- the moments of a force about a point is equal to the sum of the moments of the components of the force about the point
4.6 Moment of a Couple
- couple : two parallel forces that ahve the same magnitude but opposite directions, and are separated by a perpendicular distance.
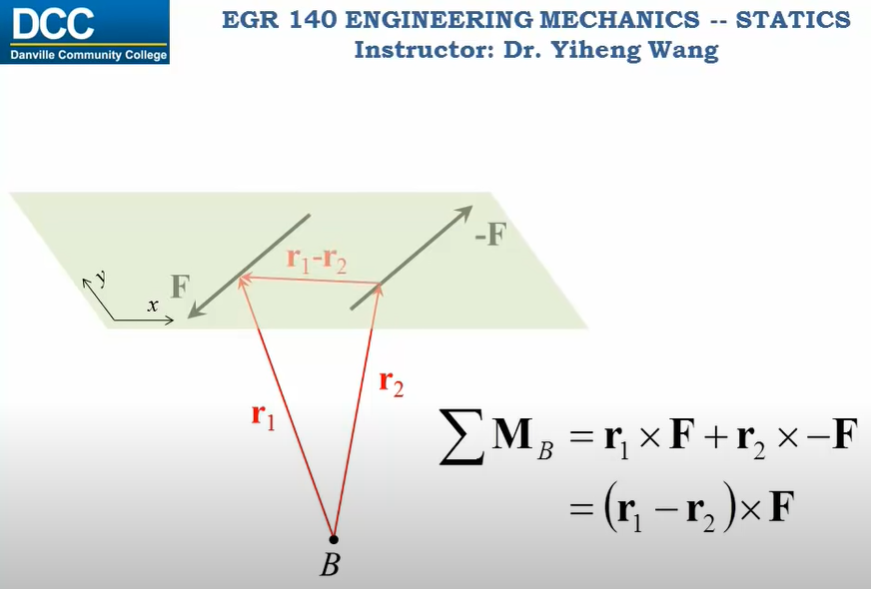
4.7 Simplification of a Force and Couple System
(1) System of Forces and Couple Moments : a system of several forces and couple moments acting on a body can be reduced to an equivalent single resultant force acting at a point O and a resultant couple moments
4.9 Reduction of a Simple Distributed Loading
- A body may be subjected to a loading that is distributed over its surface
(1) Loading along a Single Axis : \(w(x) = p(x) * b [N/m]\)
(2) Magnitude of Resultant Force
- Integration must be used since there is an infinite number of parallel forces $dF =w(x)dx = dA$ acting on the beam. The magnitude of dF is determined from the colored differential area dA under the loading curve. \(F_R = \int_L w(x)dx = \int_A dA = A\)
- The magnitude of the resultant force is equal to the area A under the loading diagram.
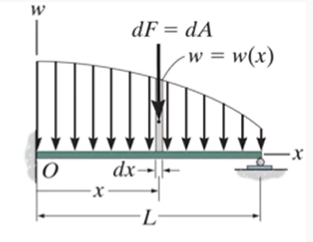
(3) Location of Resultant Force : the location $\overline{x}$ of the line of action of \(F_R\) can be determined by equating the moments of the force resultant and the parallel force distribution about the axis.
\[\overline{x} F_R = - \int_L xw(x)dx => \overline{x} = \frac{\int_L xw(x)dx}{\int_L w(x)dx} = \frac{\int_A xdA}{\int_A dA}\]
- The resultant force has a line of action which passes through the centroid C (geometric center) of the area under the loading diagram.
- Therefore, the resultant force has a magnitude equal to the volume under the loading curve p = p(x) and a line of action which passes through the centroid(geometric center) of this volume.