Chap5. Equilibrium of a Rigid Body
Objectives
- To develop the equations of equilibrium for a rigid body.
- To introduce the concept of the free-body diagram for a rigid body
- To show how to solve rigid-body equilibrium problems using the equations of equilibrium
5.1 Conditions for Rigid-Body Equilibrium
- The internal forces caused by interactions between particles within the body cancel out because these forces occur in equal but opposite collinear paris, a consequence of Newton's third law.
- The sum of the forces acting on the body is equal to zero \(F_R = \sum F = 0\)
- The sum of the moments of all the forces in the system is equal to zero \((M_R)_A = r \times F_R + (M_R)_O = 0\)
5.2 Free-Body Diagrams - 2D
- Requires a complete sepcification of all the known and unknown external forces that act on the body.
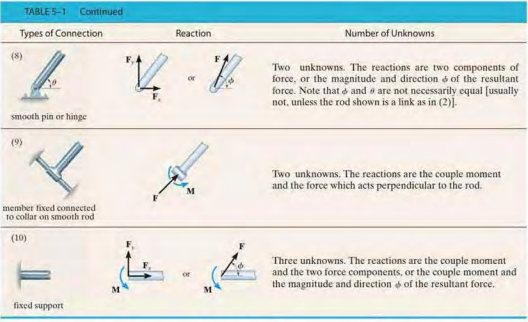
(1) Support Reactions
- If a support prevents the translation of a body in a given direction, then a force is developed on the body in that direction
- If rotation is precented, a couple moment is exerted on the body

(2) Internal Forces : The internal forces that act between adjacent particles in a body always occur in collinear pairs such that they have the same magnitude and act in opposite directions(Newton's third law).
(3) Weight and the Center of Gravity
- Each of particles has a specified weight within the gravitational field. It can be concentrated on the center of gravity
5.4 Two & Three Force Members
(1) Two force members : has forces applied at only two points on the member
- To satisfy force equilibrium, Forces must be equal in magnitude, but opposite in direction. Moment equilibrium requires forces share the same line of action.
(2) Three-Force Members
- Moment equilibrium can be satisfied only if the three forces form a concurrent or parallel force system.
5.5 Free-Body Diagrams - 3D

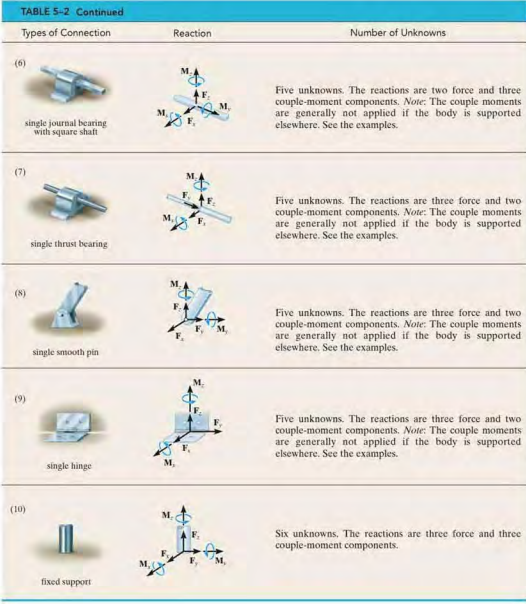
5.7 Constraints and Statical Determinacy
(1) Redundant Constraints : redundant supports become statically indeterminate : there will be more unknown lodaings on the body than euqations of equilibrium available for their solution.
- Additional equations are generally obtained from the deformation conditions at the points of support (mechanics of materials)
(2) Improper Constraints
- a body will be improperly constrained if the lines of action of all the reactive forces intersect a common axis or pass through common axis
- When the reactive forces are all parallel