Chap7. Internal Forces
Objectives
To show how to use the method of sections to determine the internal loadings in a member
To generalize this procedure by formulating equations that can be plotted so that they describe the internal shear and moement throughout a member
To analyze the forces and study the geometry of cables supporting a load
7.1 Internal Forces Developed in Structural Members
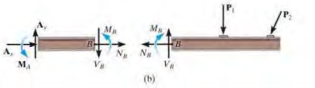
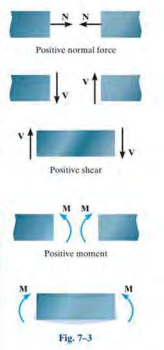
- normal force : $N_B$, acts perpendicular to the cross section
- shear force : $V_B$, acts tangential to the cross section
- bending moment : $M_B$
- The force components prevent the relative translation between the two segments, and the couple moment prevents the relative rotation. These loadings must act in opposite directions on each segment.
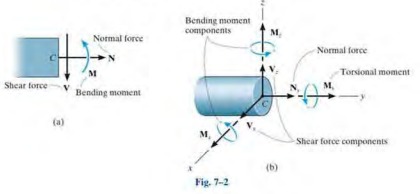
- $N_y$ : nominal force / $V_x,\ V_z$ : shear force components / $M_y$ : torsional or twisting moment / $M_x, M_z$ : bending moment components
- resultant loadings act at the geometric center or centroid of the section's cross-sectional area
7.2 Shear and Moment Equations and Diagrams
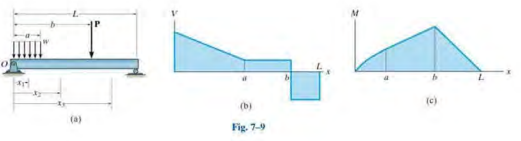
- Beams : structural members designed to support loadings applied perpendicular to their axies
- The internal shear and bendind-moment functions will be discontinuous, or their slopes will be discontinuous at points where a distributed load changes or where concentrated forces or couple moments are applied
Internal normal force is not considered for two reasons.
In most cases, the loads applied to a beam act perpendicular to the beam's axis and hence only internal shear force and bending moment are produced.
And for desing purposes, the beam's resistance to shear, and particularly to bending is more important than its ability to resist a normal force
7.3 Relations between Distributed Load, Shear, and Moment
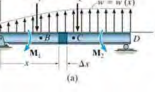
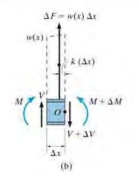
(1) Distrubuted Loads : replaced by a resultant force $w(x)\triangle x$ that acts at a fractional distance $k(\triangle x)$ from the right end, where 0<k<1
(2) Relation Between the Distributed Load and Shear
\[\sum F_y = 0; \quad V + w(x)\triangle x - (V+\triangle V) = 0 \quad \triangle V = w(x) \triangle x \\ \frac{dV}{dx} = w(x) \quad, \triangle V = \int w(x)dx\]
=> slope of shear diagram = distributed load intensity & Change in shear = Area under loading curve
(3) Relation Between the Shear and Moment
\[\sum M_O=0 \quad (M+\triangle M) - [w(x)\triangle x] k \triangle x - V \triangle x - M = 0 \\ \triangle M = V\triangle x + kw(x) \triangle x^2 \\ \frac{dM}{dx} = V, \quad \triangle M = \int V dx\]
=> slope of moment diagram = Shear & Change in moment = Area under shear diagram
(4) Force : Since the change in shear is positive, the shear diagram will jump upward when F acts upward on the beam.
(5) Couple Moment : Since the change in moment is positive, the moment diagram will jump upward if $M_0$ is clockwise.
7.4 Cables
- The weight of the cable may be neglected because it is often small compared to the load it carries, but when cables are used as transmission lines and guys for radio antenas and derricks, the cable weight may become important and must be analyzed.
Assume that the cable is perfectly flexible and inextensible.
perfectly flexible : the cable offers no resistance to bending, therefore the tensile force acting in the cable is always tangent to the cable at points along its length.
inextensible : the cable has a constant length both before and after the load is applied. => geometry unchanged and treated as a rigid body
(1) Cable Subjected to Concentrated Loads : the from of several straight-line segments, each of which is subjected to a constant tensile force
(2) Cable Subjected to a Distributed Load
$y = \frac{1}{F_H} \int (\int w(x) dx) dx$
(3) Cable Subjected to its Own Weight
\[x = \int \frac{ds}{[1+\frac{1}{F^2_H(\int w(s) ds)^2]^{1/2}}]}\]