Chap8. Friction
Objectives
- To introduce the concept of dry friction and show how to analyze the equilbrium of rigid bodies subjected to this force
- To present specific applications of frictional force analysis on wedges, screws, belts, and bearings
- To investigate the concept of rolling resistance
8.1 Characteristics of Dry Friction
Friction : a force that resists the movement of two contacting surfaces that slide relative to one another
always acts tangent to the surface at the points of contact and is directed so as to oppose the possible or existing motion between the surfaces
Dry friction(Coulomb friction) : occurs between the contacting surfaces of bodies when there is no lubricating fluid
(1) Theory of Dry Friction
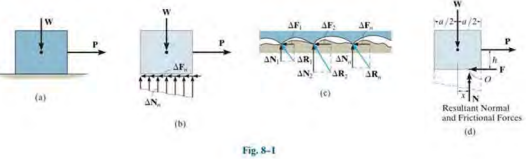
- Equilibrium
- N acts a distance x to the right of the line of action of W.
- (d) location, which coincides with the centroid or geometric center of the normal force distribution, is necessary in order to balance the "tipping effect" caused by P.
- Impending Motion
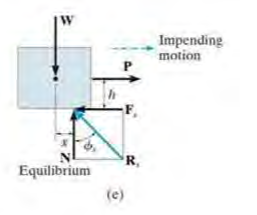
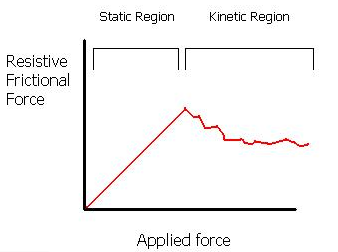
- As P is slowly increased, F correspondingly increases until it attains a certain maximum value \(F_S\), called the limiting static frictional force.
- In this state, the block is in unstable equilibrium since any furter increase in P will cause the block to move. \(μ\) is called coefficient of static friction
\[F_S = \mu_s N, \quad \phi = tan^{-1}(\frac{F_S}{N}) = tan^{-1}(\frac{\mu_S N}{N}) = tan^{-1}\mu_s\]
- Motion
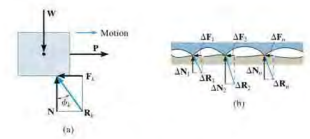
- When P is increased so that P is greater than $F_Y$, the frictional force at the contacting surface will drop to a smaller value $F_K$, called the kinetic frictional force.
- The block begins to move.
- %\mu_k% is called coefficient of kinetic friction
\[F_S = \mu_k N, \quad \phi = tan^{-1}(\frac{F_k}{N}) = tan^{-1}(\frac{\mu_k N}{N}) = tan^{-1}\mu_k\]
(2) Characteristics of Dry Friction
The frictional force acts tangent to the contacting surfaces in a direction opposed to the modtion or tendency for motion of on surface relative to another.
The maximum static frictional force is independent of contact areas when the normal pressure is not very low nor great enough to severely deform or crush the contacting surface of the body
When one of the bodies is moving with a very low velocity over the surface of another, \(μ_K\) becomes approximately equal to \(μ_s\)
8.2 Problems Involving Dry Friction
(1) Types of Friction Problems
No Apparent Impending Motion : Require the number of unknowns to be equal to the number of available equilibrium equations
Impending Motion at All Points of Contact : The total number of unknowns will equal the total number of available equilibrium equations plus the total number of available frictional equations \(F = \mu N\)
Impending Motion at Somw Point of Contact : number of unknowns will be less than the number of available equilibrium euqations plus the number of available firrctional euqations or conditional equations for tipping
=> the problem needs a determination of the kind of motion which actually occurs.
(2) Equilibirum Versus Frictional Equations
- Friction force F is to be an "equilibrium force" and satisfies the inequality $F<\mu N$
- Correct sense is made known after solving the equations of equilibrium of F.
8.3 Wedges
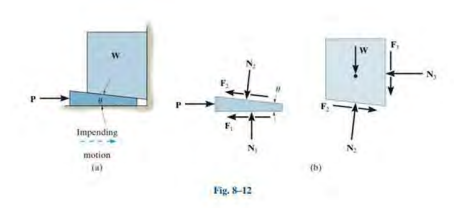
- wedge : a simple machine that is often used to transform an applied force into much larger forces directed at approximately right angles to the applied force.
8.4 Frictional Forces on Screws

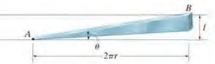
- A square-threaded screw can be considered a cylinder having an inclined square ridge or thred wrapped around it.
- lead angle : \(\theta = tan^-1 (l/2\pi r)\)
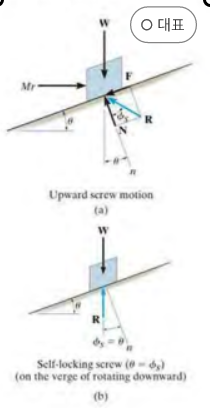
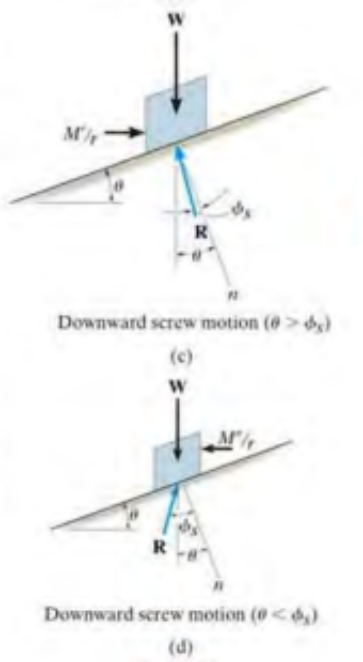
(1) Upward Impending Motion : \(M = rWtan(\phi +θ)\)
(2) Self-Locking Screw : self-locking it it remains in place under any axial load W when the moment M is removed.
(3) Downward Impending Motion : \(M =rW tan(\theta - \phi)\)
(4) Downward Impending Motion : \(M = Wr tan(\phi - \theta)\)
8.5 Frictional Forces on Flat Belts
(1) Frictional Analysis
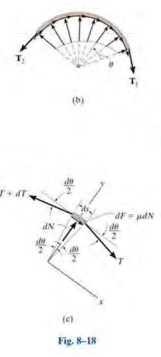
\[Tcos(\frac{d\theta}{2} + \mu dN - (T+dT)cos(\frac{d\theta}{2}) = 0 \\ dN - (T+dT)sin(\frac{d\theta}{2})-Tsin(\frac{d\theta}{2})=0\]
- $d\theta$ is infinitestimal, \(sin(\frac{d\theta}{2})=\frac{d\theta}{2}, cos(\frac{d\theta}{2})=1\)
- product of dT & \(\frac{d\theta}{2}\) is neglected
\[\therefore \mu dN = dT, \qquad dN =Td\theta \frac{dT}{T} = \mu d\theta , \quad \int^{T_2}_{T_1}\frac{dT}{T} = \mu \int^{\beta}_0 d\theta, \quad ln(\frac{T_2}{T_1}) = \mu β \\ T_2 = T_1 e^{\mu β}\]
- \(T_2\) is independent of the radius of the drum, and it is a function of the angle of belt to surface contact, \(β\)