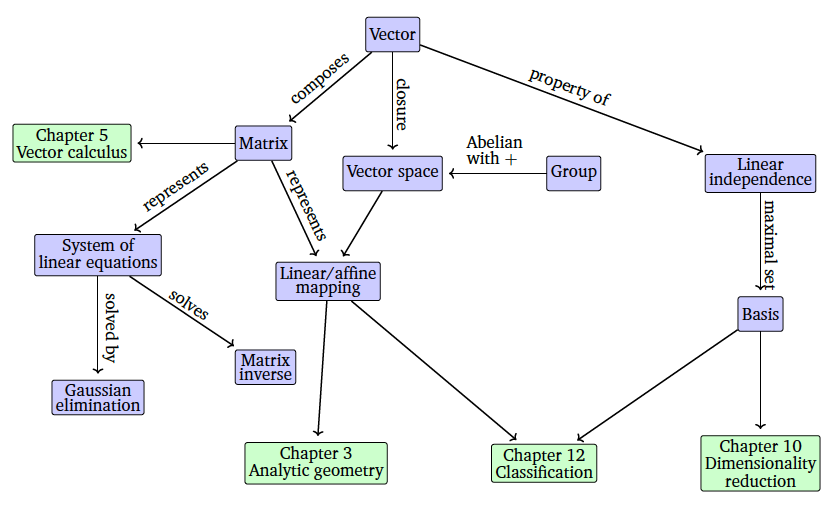
Chap2. Linear Algebra
- algebra : common approach is to construct a set of objects (symbols) and a set of rules to manipulate these objects
- polynomials are vectors → can be added and multiplied by scalar
- Considering vectors as elements of \(\R^n\)
2.1 Systems of Linear Equations
- Many real-world problems can be described with matrices & vectors.
⇒ system of linear equations.
\[a_{11}x_1+\dots+a_{1n}x_n=b_1 \\\quad... \\ a_{m1}x_1+\dots+a_{mn}x_n=b_m \]
- Geometric Interpretation
- Since a solution to a system of linear equations must satisfy all equations simultaneously, the solution set is the intersection of these lines. This intersection set can be a line (if the linear equations describe the same line), a point, or empty (when the lines are parallel).
- For three variables, each linear equation determines a plane in three-dimensional space. When we intersect these planes, i.e., satisfy all linear equations at the same time, we can obtain a solution set that is a plane, a line, a point or empty (when the planes have no common intersection).
2.2 Matrices
- Matrix : represents systems of linear equations & linear functions(linear mapping)
- With \(m, n\in \N\) a real-valued (m,n) matrix A is an m-n-tuple of elements \(a_{ij}, i=1,...,m,\ j=1,...,n\), which is ordered according to a rectangular scheme consisting of m rows & n columns.
\[A=\begin{bmatrix}a_{11} & a_{12} & ... & a_{1n} \\a_{21} & a_{22} & ... & a_{2n}\\...&...&...&... \\a_{m1} & a_{m2} & ... & a_{mn}\end{bmatrix}, a_{ij}\in\R \]
- \(\R^{m\times n}\) is the set of all real-valued (m,n)-matrices.
2.2.1 Matrix Addition & Multiplication
- For matrices \(A\in\R^{m\times n},\ B\in\R^{n\times k}\), the element \(c_{ij}\) of the product \(C=AB\in\R^{m\times k}\) are computed as
\[\displaystyle c_{ij}=\sum^n_{l=1}a_{il}b_{lj},\quad i=1,...,m,\quad j=1,...,k \]
- Matrices can only be multiplied if their “neighboring” dimensions match.
\[AB=C : (n\times k)(k\times m)=(n\times m) \]
BA is not defined if \(m\neq n\)
\(AB \neq BA\)
Matrix multiplication is not defined as an element-wise operation on matrix elements.
Identity matrix: the \(n\times n\)-matrix containing 1 on the diagonal and 0 everywhere else.
\[I_n=\begin{bmatrix}1 & 0 & ... & 0 \\0 & 1 & ... & 0\\...&...&...&... \\ 0 & 0 & ... & 1\end{bmatrix}\in\R^{n\times m} \]
Some properties of matrices:
- Associativity:
\[\forall A\in\R^{m\times n}, B\in\R^{n\times p},C\in\R^{p\times q}:\ (AB)C=A(BC)\\ \]
- Distributivity:
\[\forall A,B\in\R^{m\times n},C,D\in\R^{n\times p}:\ (A+B)C=AC+BC,\\ \qquad \qquad \qquad \qquad A(C+D)=AC+AD \]
- Multiplication with the identity matrix:
\[\forall A\in\R^{m\times n}:\ I_mA=A_n=A \]
2.2.2 Inverse and Transpose
< Inverse Matrix >
Consider a square matrix \(A\in\R^{n\times n}\). Let matrix \(B\in\R^{n\times n}\) have the property that \(AB=I_n=BA\). B is called the inverse of A and denoted by \(A^{-1}\).
- If inverse matrix does exist, A is called regular, invertible, nonsingular, otherwise singular, noninvertible
- When the matrix inverse exists, it is unique
< Transpose >
For \(A\in\R^{m\times n}\), the matrix \(B\in\R^{n\times m}\) with \(b_{ij}=a_{ij}\) is called the transpose of A. \(B=A^T\)
- Important properties of inverses and transposes
\[AA^{-1}=I=A^{-1}A\\(AB)^{-1}=B^{=1}A^{-1}\\(A+B)^{-1}\neq A^{-1} + B^{-1}\\(A^T)^T=A\\(A+B)^T=A^T+B^T\\(AB)^T=B^TA^T \]
< Symmetric matrix >
A matrix \(A\in \R^{n\times n}\) is symmetric if \(A=A^T\)
- only (n,n)-matrices can be symmetric.
- Sum of symmetric matrices \(A,B\in \R^{n\times n}\) is always symmetric, but their product is generally not symmetric.
2.2.3 Multiplication by a Scalar
Let \(A\in\R^{m\times n}&λ\in\R.\ Then\ λ A=K,\ K_{ij}=λ a_{ij}\).
- Associativity
\[(λ \psi)C=λ(\psi C),\quad C\in\R^{m\times n} \\ λ(BC)=(λ B)C=B(λ C)=(BC)λ,\quad B\in\R^{m\times n},\ C\in\R^{n\times k}\\(λ C)^T=C^Tλ^T=C^Tλ=λ C^T\]
- Distributivity
\[(λ +\psi)C=λ C+\psi C, C\in\R^{m\times n} \\λ(B+C)=λ B+λ C,\ B,C\in\R^{m\times n} \]
2.2.4 Compact Representations of Systems of Linear Equations
- Generally, a system of linear equations can be compactly represented in their matrix form as Ax = b.
2.3 Solving Systems of Linear Equations
2.3.1 Particular and General Solution
- paricular solution : a vector that satisfies Ax=b whether the solution is unique
- general solution : all solutions of the equation system
The general approach
- Find a particular solution to \(Ax=b\)
- Find all solutions to \(Ax=0\)
- Combine the solutions from steps 1. and 2. to the general solution
- neither the general nor the particular solution is unique
2.3.2 Elementry Transformations
- keep the solution set the same, but that transform the equation system into a simpler form
- Exchange of two equations (rows in the matrix representing the system of equations)
- Multiplication of an equation (row) with a constant \(λ \in\R{0}\)
- Addition of two equations (rows)
augmented matrix : \([A|b]\)
pivot : the leading coefficient of a row (first nonzero number from the left)
⇒ always strictly to the right of the pivot of the row above → any equation system in row-echelon form always has a “staircase” structure
< row-echelon form >
- All rows that contain only zeros are at the bottom of the matrix; correspondingly, all rows that contain at least one nonzero element are on top of rows that contain only zeros.
- Looking at nonzero rows only, the first nonzero number from the left(pivot or the leading coefficient) is always strictly to the right of the pivot of the row above it.
- basic variables : variables coresponding to the pivots in the row-echolon form / others: free variables
- Reduced Row Echelon Form
- It is in row-echelon form
- Every pivot is 1.
- The pivot is the only nonzero entry in its column.
- Gaussian elimination is an algorithm that performs elementary transformations to bring a system of linear equations into reduced row-echelon form.
2.3.3 Calculating the Inverse
- Need to find a matrix X that satisfies \(AX=I_n\), then \(X=A^{-1}\)
- Use augmented matrix notation
\[[A|I_n]\rightarrow[I_n|A^{-1}] \]
→ Determining the inverse of a matrix is equivalent to solving systems of linear equations
2.3.4 Algorithms for Solving a System of Linear Equations
Assume that a solution exists, and it is able to determine the inverse \(A^{-1}\) → only possible when A is a square matrix and invertible
Otherwise, under mild assumptions ( A needs to have linearly independent columns)...
\[Ax=b \rightarrow A^TAx=A^Tb\rightarrow x=(A^TA)^{-1}A^Tb \]
→ and use the Moore-Penrose pseudo-inverse \((A^T A)^{-1} A^T\) ⇒ minimum norm least-squares solution.
It requires many computations for the matrix-matrix product & computing the inverse of \(A^T A\)
Gaussian elimination plays an important role when computing determinants, checking whether a set of vectors is linearly independent, computing the inverse of a matrix, computing the rank of a matrix, and determining a basis of a vector space.
- it is impractical as the required number of arithmetic operations scales cubically in the number of simultaneous equations.
In practice, systems of many linear equations are solved indirectly, by iterative methods.
2.4 Vector Spaces
2.4.1 Groups
Group : Consider a set \(G\) and an operation : \(\otimes: G \times G \rightarrow G\) defined on \(G\). Then \(G:=(G,\otimes )\) is called a group if the following hold:
- Closure of \(G\) under \(\otimes: \forall x, y \in G : x \otimes y \in G\)
- Associativity : \(\forall x,y,z \in G : (x \otimes y) \otimes z = x \otimes (y \otimes z)\)
- Neutral element : \(\exist e \in G,\ \forall x \in G : x \otimes e = x\ and\ e \otimes x = x\)
- Inverse element : \(\forall x \in G,\ \exist y \in G : x\otimes y = e\ and\ y \otimes x = e\) where e is the neural element. We often write \(x^{-1}\) to denote the inverse element of x.